본 포스트는 cs231n 6강 리뷰입니다.

Traning Neural Network 1

Previous On cs21n

지난 시간 데이터 입력이 들어오면 W와 곱합니다. Wx는 FC나 CNN이 될 수도 있죠 그 다음 활성함수 즉 비선형 연산을 거치게 됩니다

Activation Functions(활성 함수)

Sigmoid
Sigmoid는 각 입력을 받아서 [0,1] 값이 되도록 해줍니다. 입력값이 크면 1에 가깝게 아니면 반대로 0 근처 구간을 보면 선형함수 같아 보입니다(/부분) 시그모이드가 뉴런의 활성률을 saturation(극단값을 갖도록)시키는 것으로 해석할 수 있습니다. 어떤 값이 0-1사이의 값을 가진다면 이것을 활성률이라고 생각할 수 있다

문제점

Saturation 뉴런이 graidents를 죽입니다 x가 너무 작거나 클 경우에 시그모이드에서 0으로 수렴하게된다
그래서 0값이 backprop을 진행하면서 0에 가까운값을 갖게 될 것입니다 그리고 이 0 graident가 계속 내려갑니다
시그모이드 출력이 not Zero Centered 모든 input이 양수라면 graident는 전부 ‘양수’ 또는 ‘음수’가 됩니다.
이것이 의미하는 것은 W가 모두 같은 방향으로만 움직일 것입니다 파라미터를 업데이트할 때 다같이 증가하거나 감소하거나
이 문제는 매우 비효율적인 문제가 있습니다.
exp()로 인해 계산 비용이 크다
그렇게 큰 문제는 아님

tanh
범위는 [-1,1] 시그모이드와의 큰 차이점은 Zero-centered

문제점

여전히 kill gradients

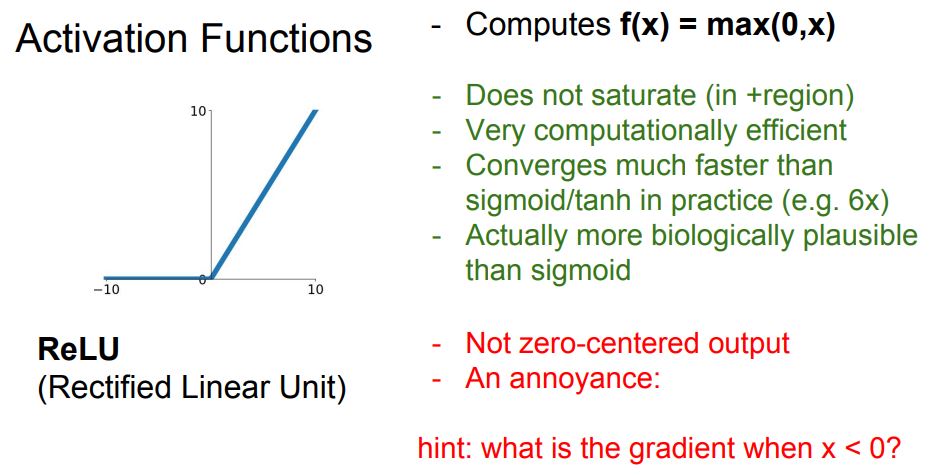
ReLU

f(x)=max(0,x)

보시는바와 같이 입력이 음수면 0 양수면 입력값 그대로를 출력합니다. 특징

입력의 절반은 saturation 되지 않는다
계산효율이 높다 단순한 max연산이기에 빠르다 (6배정도)
생물학적 타당성이 Sigmoid보다 크다.

문제점

Not Zero Centered
음수일경우에 Saturation된다

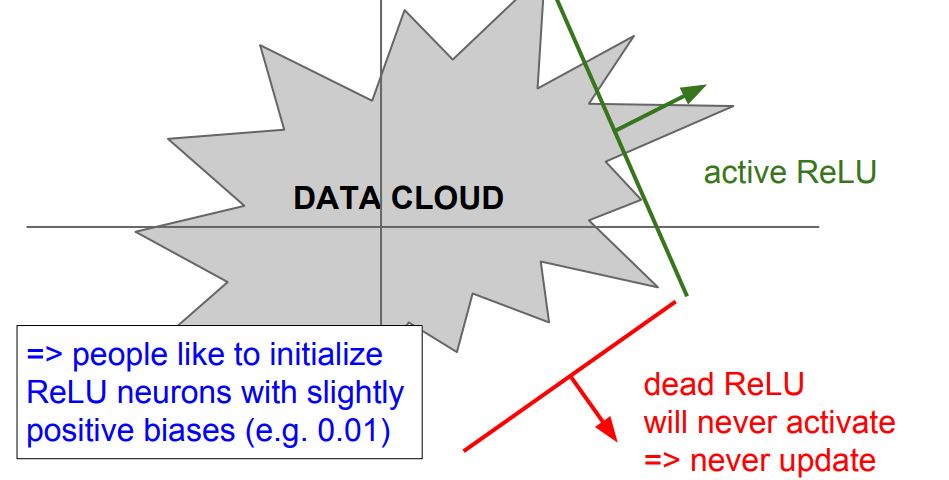
Dead ReLU 이유

초기화를 잘못한 경우
가중치 평면이 data cloud에서 멀리 떨어진 경우
Learning rate가 너무 높을 경우 처음엔 적절하게 시작해도 update를 크게 해버려 가중치가 뛰어 데이터의 manifold를 벗어나게 됩니다.(처음에 학습 잘 되다가 갑자기 죽어버리는 경우)

Leaky ReLU
$f(x)=max(0.01x,x)$

기존 ReLU와 유사하지만 음수인 경우 기울기를 살짝 주게 되면서 문제점을 해결합니다 이제 음수인 영역에서도 saturation되지 않습니다.
Dead ReLU 현상도 없습니다.

PReLU(Parametric Rectifier)
$f(x)=max(\alphax,x)$

여기서 alpha는 backprop과정 속에서 학습시키는 파라미터로 만든 것입니다

ELU
ELU는 ReLU와 Leaky ReLU의 중간

ReLU의 장점을 갖고있으면서도 zero nmean에 가까운 출력
하지만 여기서 음수영역은 또 다시 saturation됩니다.
그들은 이 방법이 noise에 더 강인함을 줄 수 있다고 주장합니다.

Maxout “Neuron”
입력을 받는 특정한 형식을 미리 정의하지 않습니다. ReLU와 Leaky ReLU의 좀 더 일반화된 형태입니다. 왜냐하면 두 개의 선형함수를 입력으로 받기 때문입니다.
선형이기 때문에 saturation되지 않습니다.

문제점

뉴런당 파라미터 수가 두배가 된다
W1과 W2를 지니고 있어야하기 때문에

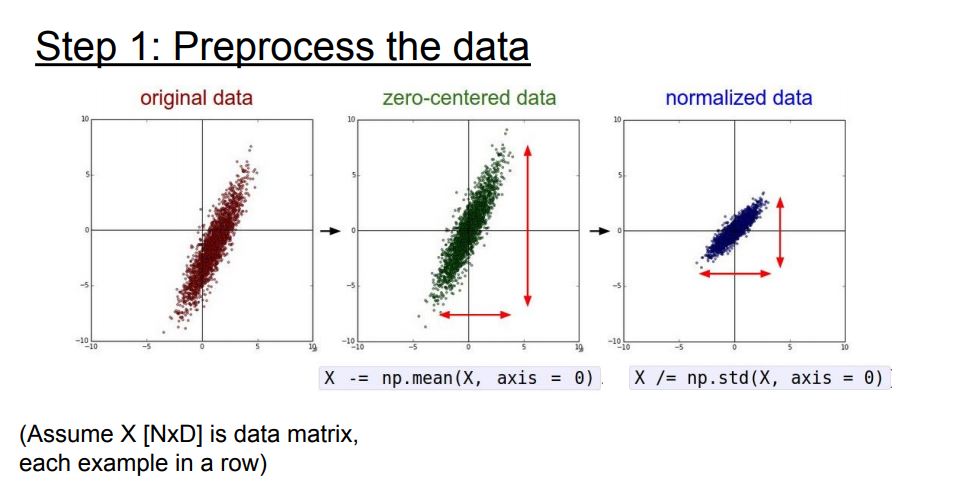
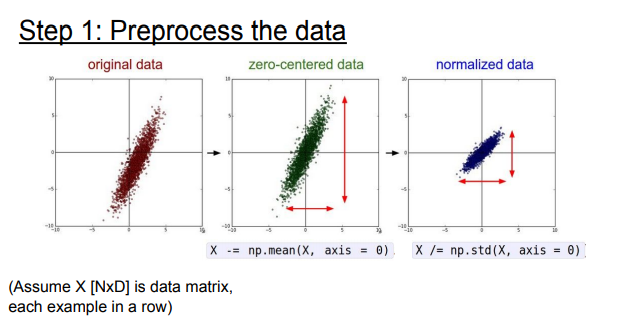
Data Preprocessing

일반적으로는 입력 데이터는 전처리를 해줍니다

대표적인 전처리 과정

Zero-mena으로 만들기
Normalize - 데이터를 동일한 범위안에 있게 해줘서 동등하게 활용될 수 있도록 해줌

이미지는 zero-centering 정도 까지만!!
이미 각 차원간에 스케일이 어느정도 맞쳐줘있기 때문에 이미지를 다룰 때는 굳이 입력을 더 낮은 차원으로 projection 시키지 않습니다 채널 전체의 평균 대신 채널마다 독립적으로 평균을 계산하는 경우도 있습니다.

Sigmoid 문제점을 해결할 수 있을까?

zero-mean을 활용하면 첫 번째 레이어에서만 해결할 수 있습니다
그 다음 레이어부터는 똑같은 문제가 반복될 것입니다.
Sigmoid 문제를 해결하기엔 충분하지 않습니다.

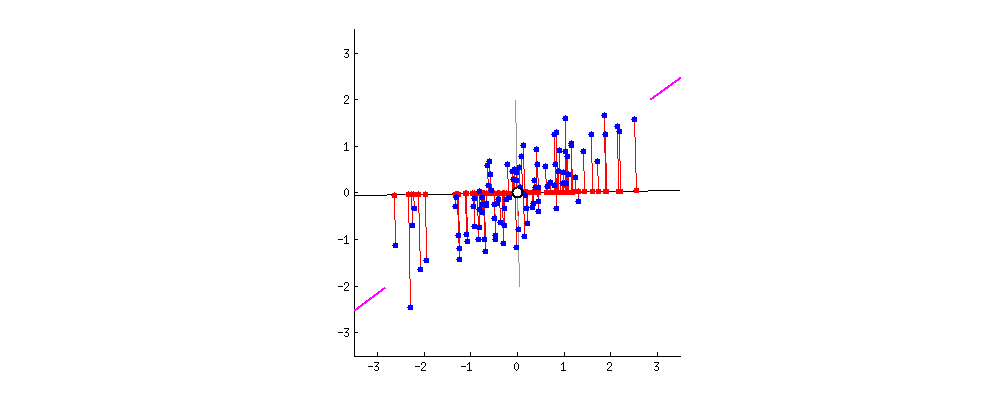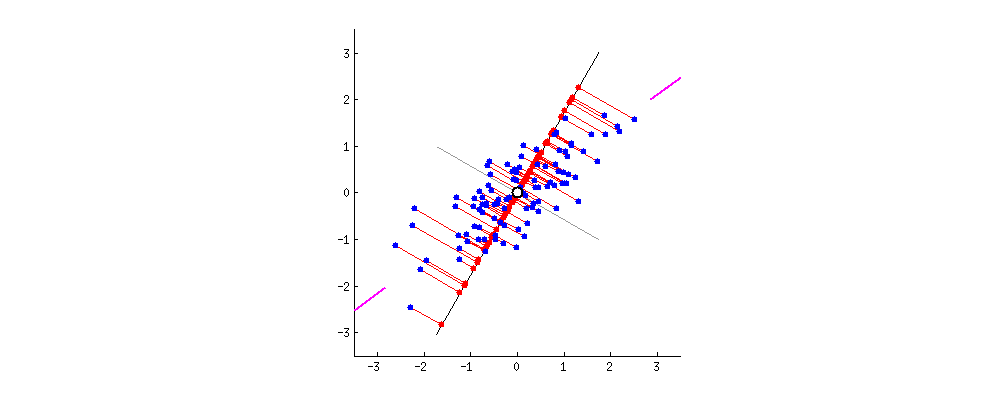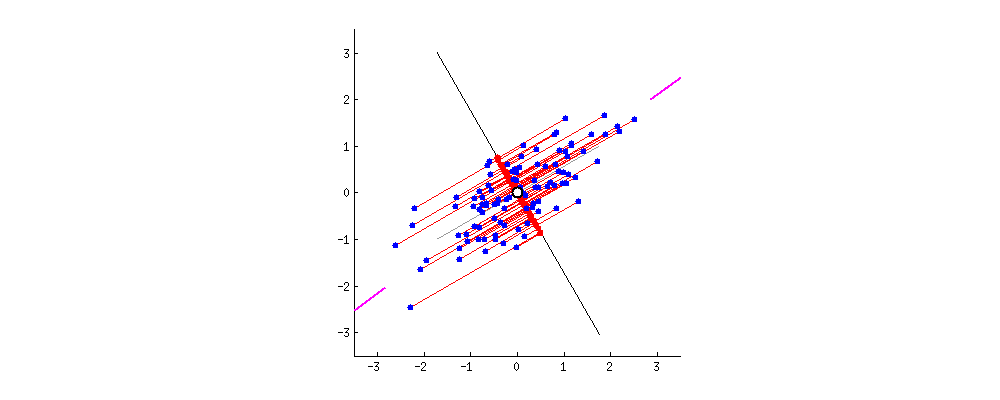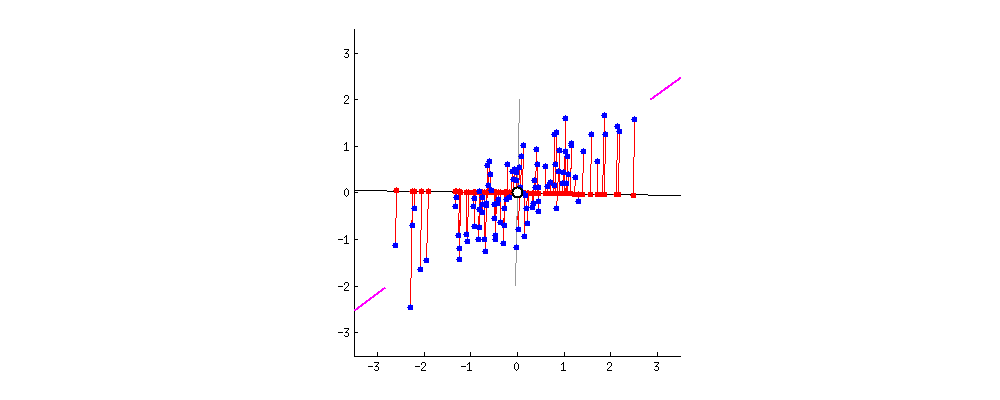
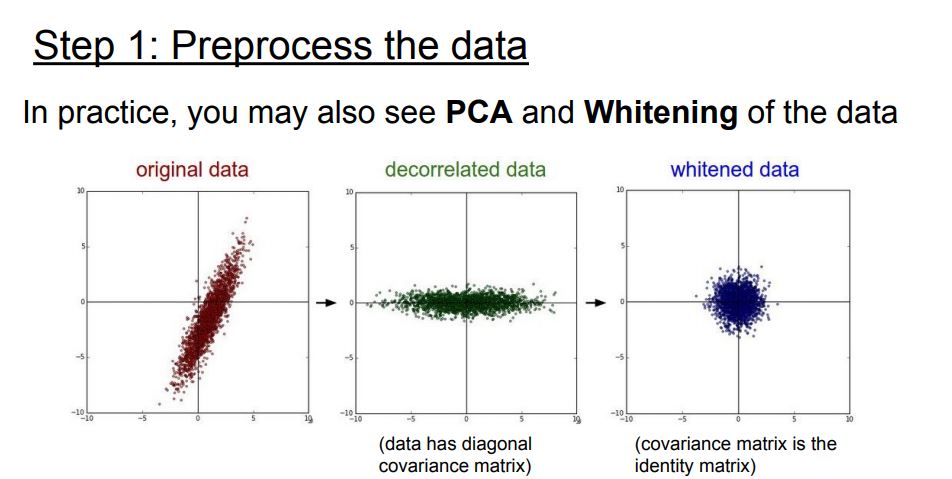
PCA(Principal Component Analysis)
PCA는 데이터의 분산(variance)을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아, 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법입니다. 데이터를 정규화 시키고 공분산(Covariance) 행렬을 만든다. 공분산 행렬이란 각 구조간 상관관계를 말해주는 행렬이다.

Whitening
들어오는 입력값의 feature들을 uncorrelated하게 만들어주고 평균은 0 분산은 단위행렬을 갖게 만들어주는 작업이다.
작업 중 covariance matrix 계산과 inverse 계산량이 많고 Whitening을 거친 이후 일부 파라미터들의 영향이 무시되는 문제점이 있다.

[흔히 하는 실수]
전처리 기법을 적용함에 있어서 명심해야 하는 중요한 사항은 전처리를 위한 여러 통계치들은 학습 데이터만 대상으로 추출하고 검증, 테스트 데이터에 적용해야 한다.

Weight Initialization

맨 처음에 어떤 초기 가중치들이 있습니다.
그리고 Gradient를 계산해서 가중치를 업데이트할 것입니다.
모든 가중치가 0이면 어떻게 될까요?

모든 뉴런은 모두 다 같은 연산을 수행합니다.
출력도 모두 같을테고 결국 Gradient도 같고 모든 뉴런이 똑같이 생길것입니다.
* Symmetry braking이 일어나지 않습니다!!

Symmetry braking란?

Symmetry breaking은 신경망과 같은 기계 학습 모델을 초기화하는 요구 사항을 나타냅니다.

몇몇의 머신러닝 모델들이 모두 같은 값으로 가중치가 초기화 되었을 때, 모델마다 가중치들이 다르게 학습되어지지 않거나 어려워질 수 있습니다 이것을 “Symmetry”라고 합니다

모델을 랜덤한 작은 값으로 초기화하는 것은 “Symmetry” 깨부숩니다. 그리고 다른 가중치가 독립적으로 학습할 수 있도록 해줍니다.

출처:https://machinelearning.wtf/terms/symmetry-breaking/

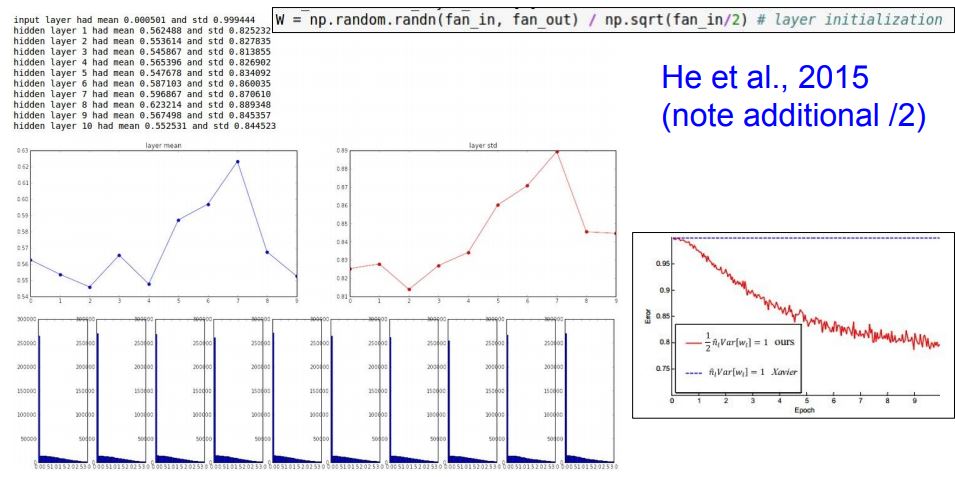
1번 임의의 작은 값으로 초기화 하자(가우시안)
W= 0.01*np.random.randn(D,H)
이 경우 표준정규분포로 해줍니다
작은 네트워크라면 이정도면 충분합니다.

but, 깊은 네트워크인 경우 문제가 생길 수 있습니다.

예시

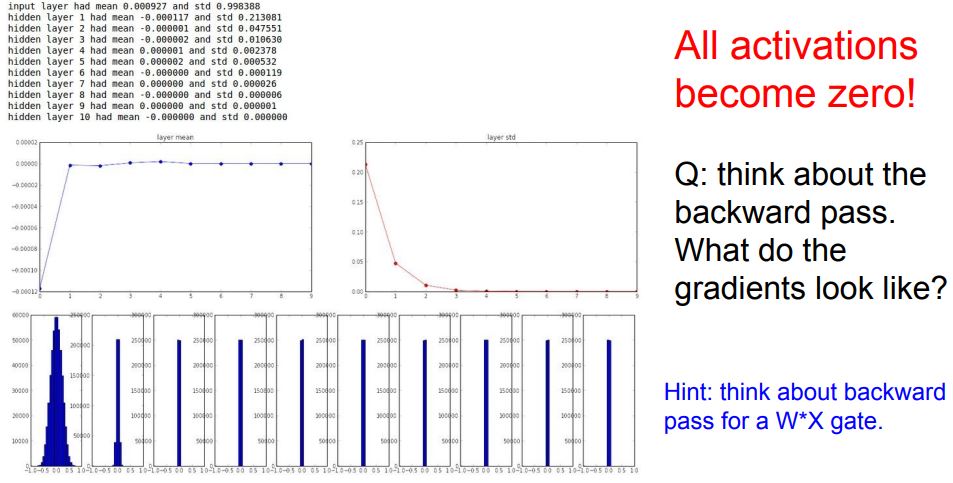
데이터를 랜덤으로 만들고 forward pass 진행
각 레이어별 activations 수치를 통계화

결과는 각 레이어 출력의 평균과 표준편차입니다.
1번 레이어는 평균이 0근처입니다(tanh 특성상),표준편차를 보면 가파르게 줄어드는것을 확인할 수 있습니다.
1번 레이어의 그래프는 예븐 가우시안 분포로 되어있지만 갈수록 W가 너무 작은 값들이라서 출력값이 급격히 줄어듭니다.
결국 0이 되버리겠죠..

backward pass
현재 가중치=upstream gradient _ local gradient
local gradient = WX에서 W에 대하여 미분 = X
upstream gradient = 현재 upstream(backprop로 노드로 흘러 들어온 것) _ W
X= 매우 작은 값 -> gradient 작은 값 -> 업데이트 잘 안됨

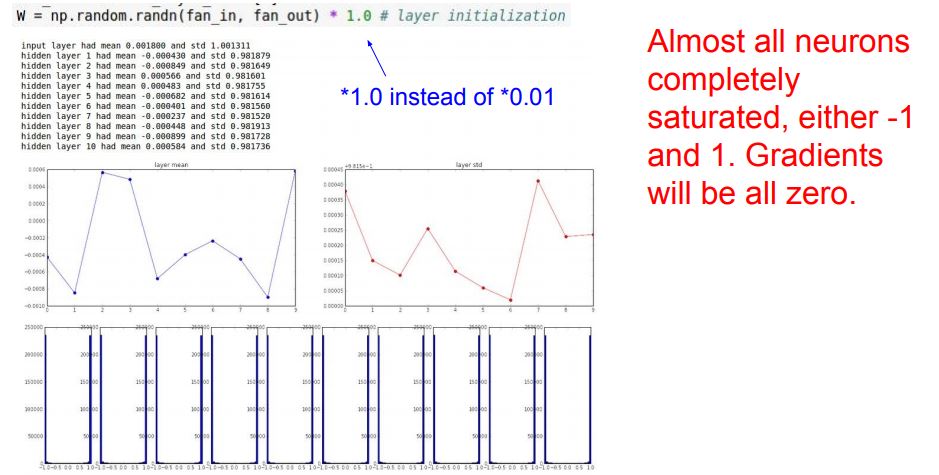
반대로 가중치가 큰 경우
값들이 saturation될 것 출력이 항상 -1 or +1

그렇다면 가중치는 어떻게 초기화 해야할까요??

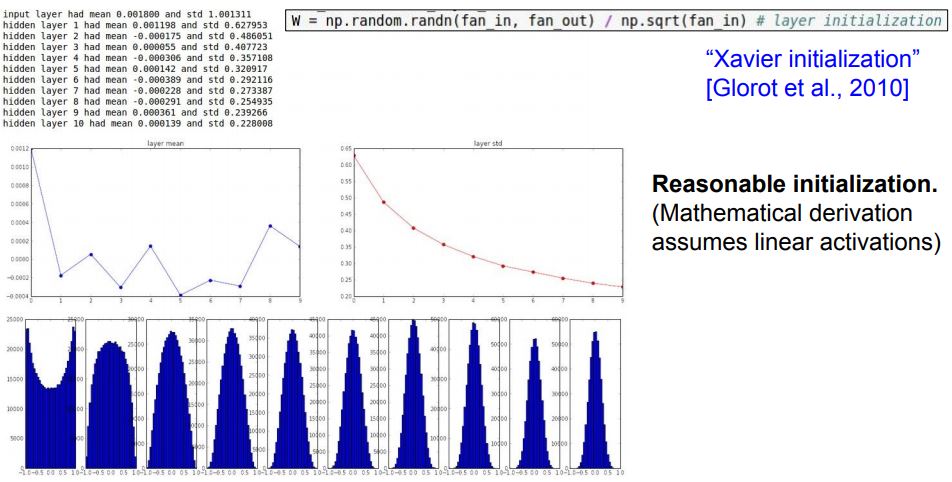
Xavier initialization[Glorot et al., 2010]
가우시안으로 뽑은 값을 입력의 수로 스케일링 해줍니다.
기본적으로 입/출력의 분산을 맞춰주는 일을 합니다. 가정: Linear activation이 있다.

입력의 수가 작으면 더 작은 값으로 나뉘어 더 큰 값을 얻습니다. 더 큰 값이 필요한 이유는 작은 입력의 수가 W와 곱해지기 때문에 가중치가 더 커야 출력의 분산 만큼 큰 값을 얻을 수 있기 때문입니다.

but, ReLU를 쓰면 잘 작동되지 않는다. 왜냐면 출력의 절반을 날려먹기 때문에
이 문제를 해결하기위해 입력의수/2를 해줍니다 위에서 말했듯이 절반만 들어가기 때문입니다.

Batch Normalization

가우시안의 범위로 activation을 유지시키는 또 다른 방법!

어떤 레이어로 부터 나온 Batch 단위 만큼의 출력의 분포가 Unit gaussian이면 좋을 것 같습니다.(Weight를 바꾸는게 아니에요!)
가중치를 잘 초기화 하는 것 대신에 학습 때 마다 각 레이어에 현재 Batch에서 계산한 mean과 variance를 이용해서 Normalization을 해줘서 모든 레이어가 Unit Gaussian이 되도록 해줍니다.

각 뉴런을 평균과 분산으로 Normalization해주는 함수로 구현하는 것
평균과 분산을 ‘상수’로 가지고만 있으면 언제든 미분이 가능하기 때문에 Backprop이 가능합니다

Batch 당 N개의 학습 데이터, 각 데이터는 D차원
각 차원별로 평균을 각각 구함 -> 한 Batch에서 전부 계산 후 Normalize

깊은 네트워크에서는 레이어의 W가 곱해지면서 스케일이 안좋은 방향으로 학습이 진행 됐는데 이 BN이 그것을 상쇄시킵니다.
또한 BN은 입력의 스케일만 살짝 조정하는 역할이기 때문에 FC와 Conv 직후 어디에든 적용할 수 있습니다.
다만 Conv layer에선 독립적으로 수행하는 것이 아니라 Activation map에 같은 채널에 있는 요소들은 같이 Normalize해줍니다

과연 layer를 거칠 때 마다 Normalization하는것이 좋은건가?
왜하는거지?
tanh의 입력이 unit gaussian이기를 바라는 건가?
Normalization의 역할은 입력이 강제로 tanh의 linear한 영역에만 있도록 하는 것입니다.
그럼 saturation이 일어나지 않겠죠, but saturation을 조절할 수 있다면??

Normalize된 값들을 감마로 스케일링 효과, 베타는 이동 효과를 줍니다.
다시 원상복구를 하고 싶다면 감마=분산, 베타=평균으로 하면 됩니다.

BN은 gradient의 흐름을 원활하게 해주며 결국 더 학습이 잘되게 해줍니다.
learning rate 키울수 있고 다양한 초기화 기법을 사용할 수 있습니다.
또한 Regularization 역할도 합니다. 각 레이어의 출력은 batch안에 존재하는 모든 데이터들에 영향을 받습니다(batch의 평균에 영향을 받기 때문)

Babysitting the Learning Process

학습과정을 어떻게 모니터링하고 하이퍼파라미터를 조절할 것인지에 대하여

Loss funtion

데이터 전처리 (Zero-mean)
아키텍쳐 선택(1 Hidden layer, 50 neurons)
네트워크 초기화

Softmax classifier의 Loss는 negative log likelihood가 되어야 합니다.
* 10개의 클래스가 있다면 -log(1/10)
아래는 Regularization을 증가시킨 것입니다. 그래서 Loss 값이 증가한 것을 볼 수 있습니다.

학습 준비 끝!!

전체 학습을 시작하기 전에 잘 만들어졌는지 확인해보는 작업입니다.

20개 샘플만 사용(CIFAR-10) overfit되기 쉽고 loss는 0으로 수렴할것으로 예상
reg=0.0
sgd 사용 Accuracy가 1.0까지 올라갔습니다.

이제 전체 데이터셋을 사용하며 reg를 올려주고 적절한 learning rate를 찾아야합니다.
learning rate는 중요한 하이퍼파라미터중 하나이면서 가장 먼저 정해주어야 합니다.

Softmax 사용중에 loss가 크게 변하지 않았음에도 불구하고 Accuracy는 왜 올라간것일까요?
현재 상황은 확률 값들이 아직까지 멀리 퍼져있고 loss는 여전히 비슷비슷한 수준입니다. 하지만 저희는 학습을하고 있기 때문에 조금씩 “옳은” 방향으로 바뀌고 있습니다.
가중치는 서서히 변하지만 Accuracy는 갑자기 뛰어버릴 수 있습니다. 그 이유는 Accuracy는 가장 큰 값만 취하기 때문입니다

learning rate가 너무 큰 경우에는 NaN값이 출력됩니다. NaN은 Cost가 발산하는 것을 의미합니다.
보통 learning rate는 1e-3 ~ 1e-5 사이의 값을 사용합니다.

왼쪽 : 다양한 학습률의 효과를 보여줍니다.

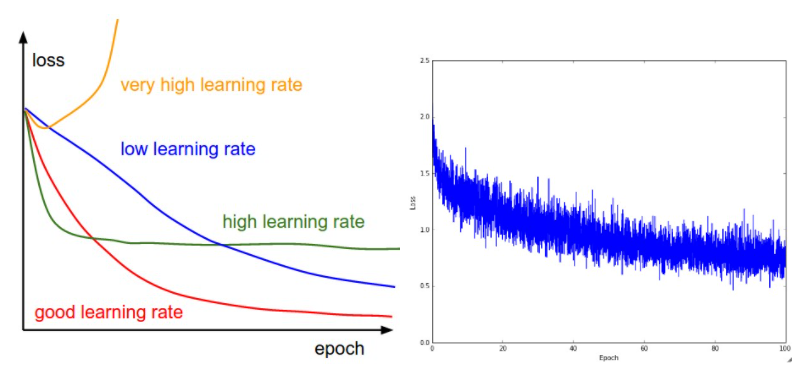
학습률이 낮으면 선형적으로 개선됩니다.
높은 학습률로 그들은 더 기하급수적으로 보일 것입니다.
학습률이 높을수록 Loss가 더 빨리 줄어들지만 더 안좋은 손실 값 (녹색선)에 갇히게됩니다. 최적화 환경에서 좋은 위치에 정착 할 수 없기 때문입니다. 이 이야기는 산을 내려갈 때의 예시를 떠올리시면 이해가 쉬울 것입니다.
오른쪽 : CIFAR-10 데이터 세트에서 소규모 네트워크를 훈련하는 동안 시간에 따른 일반적인 loss funtion을 나타낸 것.
이 손실 함수는 합리적으로 보이며 (감쇠 속도에 따라 학습률이 약간 낮다는 것을 나타낼 수 있지만 말하기는 어렵습니다) 배치 크기가 약간 낮을 수도 있음을 나타냅니다 (cost가 작고 노이즈가 심하기 때문에).

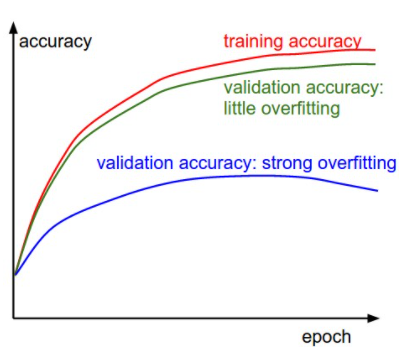
training accuracy와 validation accuracy 사이의 차이는 과적합 정도를 나타냅니다. 두 가지 가능한 경우가 왼쪽에 나와 있습니다.
파란색 선은 초록색 선보다 매우 작은 정확도를 보여 주며 이는 강력한 과적합을 나타냅니다 (참고 : validation accuracy가 어느 시점 이후에 내려 가기 시작할 수도 있음).

실제로 이것을 볼 때 정규화를 늘리거나 (더 강력한 L2 가중치 패널티, 더 많은 드롭 아웃 등) 더 많은 데이터를 수집하고 싶을 것입니다.
다른 가능한 경우는 validation accuracy가 training accuracy를 상당히 잘 추적하는 경우입니다. 이 경우는 모델 용량이 충분히 높지 않음을 나타냅니다. 매개 변수 수를 늘려 모델을 더 크게 만듭니다.

Hyperparameter Optimization

하이퍼파라미터를 최적화하는 전략중 하나는 Cross-validation을 이용하는 것입니다.
Training set으로 학습시키고 validation set으로 평가합니다.

\1. Coarse stage 우선 Coarse stage에서는 넓은 범위에서 값을 골라냅니다. 적은 Epoch만으로도 현재 값이 잘 동작하는 지 알 수 있습니다.(Cost가 줄어드는지 Accuracy가 증가하고 있는지 확인해 보며) \2. fine stage
좀 더 좁은 범위를 설정하고 Epoch를 늘려 최적의 값을 찾습니다.

하이퍼 파라미터 최적화할 때는 Log scale로 값을 주는 것이 좋습니다. 샘플링할 때 10e-3~10e-6 대신 10의 차수 값만 -3 ~ -6 왜냐하면 learning rate는 gradient와 곱해지기 때문에 선택 범위를 log scale을 사용하는 편이 좋습니다.

빨간색 화살표를 보시면 acc값은 가장 좋지만 한 가지 문제가 있습니다. learning rate가 모두 10e-4 사이에 존재하고 있습니다.
learning rate의 최적값들이 2번에 따른 범위의 경계부분에 집중되어 있는데 이것을 좋지 않습니다. 이렇게 되면 최적의 learning rate를 탐색할 수 없을 수 있기 때문입니다. 실제로 최적값이 10e-4나 10e-6에 위치해 있을 수도 있기 때문입니다. 최적의 값은 정한 범위의 중앙에 위치하도록 범위를 잘 설정해주는 것이 중요합니다.

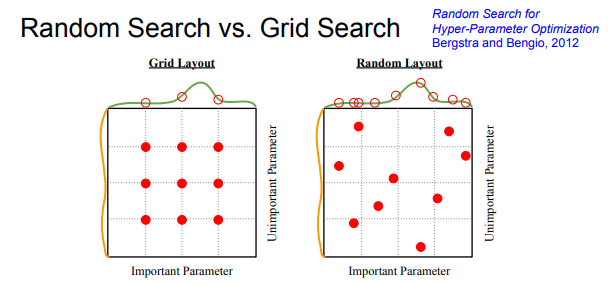
또 다른 방법으로는 흔히 알고 있는 Grid Search 방법입니다.
하이퍼파라미터를 고정된 값과 간격으로 샘플링 하는 것입니다. 하지만 실제로는 random하게 찾는것이 더 좋습니다.

이유: 내 모델이 어떤 특정 파라미터의 변화에 더 민감하게 반응한다고 가정한다면(노랑<초록) 중요한 파라미터(초록, 잘 반응하는)에게 더 많은 샘플링이 가능하기 때문입니다. 반대로 Grid layout에서는 3번밖에 탐색하지 않기 때문에 어느 부분이 좋은 지역(rigon)인지 알 수 없습니다. 결국 Random Search를 사용하면 중요한 variable에서 더 다양한 값을 샘플링 할 수 있기 때문에 좋습니다

Up page Button